Authors: Nitai S. Dasa, Hillol Joardara, Matruprasad Routb, Bikash C. Beheraa, Kalipada Maity
Abstract
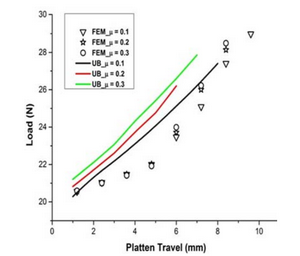
This paper outlines the salient features of the “generalized upper bound” technique and uses it to derive upper bounds for plane strain compression and extrusion of metals in the presence of Coulomb friction (τ = µp). For compression the velocity field is established by reformulating the same proposed earlier by Lee and Altan so as to be compatible with the interface Coulomb friction condition. For extrusion, the upper bound velocity field is derived from a stream function for flow through a smooth die of wedge angle (α+λ) where, α is the semi-wedge angle of the rough die, and λ is the friction angle (tanλ = µ). Analysis for this case is also presented assuming the flow to be radial. The analytical results are compared with those obtained from, the slip-line field and finite element analyses and from the rigid triangle velocity fields. These are also validated by some e experimental results available in literature.
Key words: Coulomb friction; Upper bound; Plain strain; stream function compression; extrusion; Finite element modelling
DOI: 10.24867/ATM-2021-2-002
